원과 파이

 

 

 

 

동그란 원 이름 정하기

 

원이라는 도형에 대해서 이런 저런 생각을 해볼까요?

 

원을 보면서 이름을 정해주고 싶은 부분들을 찾아봅니다.

 

원은 딱 보면 동그랗게 보이니까

 

이 동그란 물체를 포장하려고 하는데 

포장지를 준비하려면 한바퀴 돌리는데 필요한 길이를 알아야 할텐데

둘레는 몇 cm 일까?

 

이 동그란 물체를 어디에 보관하고 싶은데

공간을 준비하려면 가로지르는 길이를 알아야 할텐데

가로지르는 길이는 몇 cm 일까?

 

이 동그란 물체를 색칠하고 싶은데 

보이는 면의 전체 넓이를 알아야 할텐데

전체 면적은 몇 제곱 cm 일까?

 

 

관심 있는 곳들에 대해

하나씩 이름을 정해보자.

 

한바퀴 돌리는 둘레 길이는 원주라고 하고

간단하게 L 이라고 적어보자.

 

가로지르는 길이는 지름이라고 하고

D 라고 해보자.

 

전체 넓이는 면적이라고 하고 

S 라고 적어보자.

 

 

 

 

 

 

쪼개진 원 이름 정하기

 

원이 쪼개지니까

이름을 정해줘야 하는 것들이 더 남아있네요.

 

 

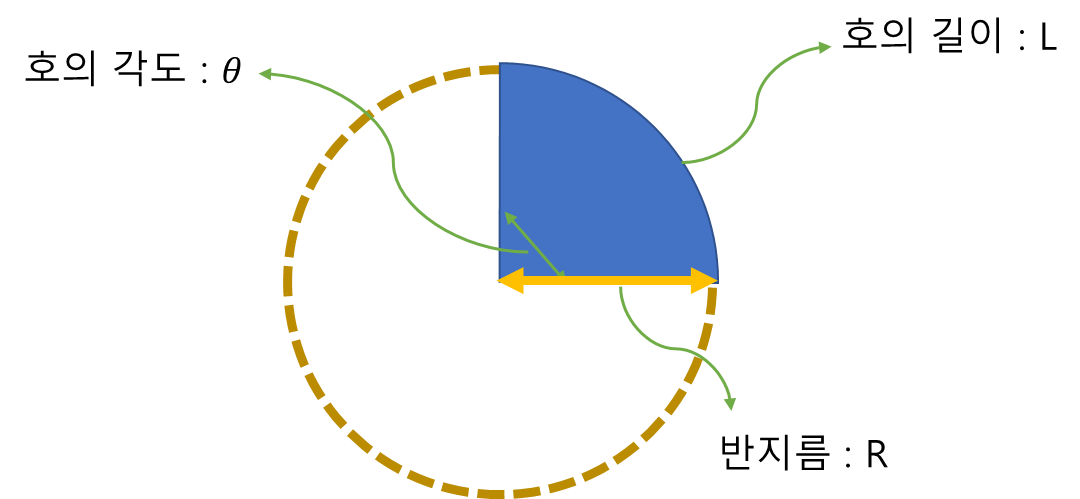
피자의 손잡이에 해당하는 걸 호라고 정하고

L 이라고 적어보자. 

 

피자의 꼭지에 해당하는 부분은 길이로 표현하기 힘드니 

호의 각도라고 정하고 

세타 라고 적어보자.

 

 피자 조각의 옆부분의 길이는 전체 피자판의

반지름에 해당하니

R 이라고 적어보자. 

 

 

 

 

 

관계 정하기

 

이름을 정했으니 이걸로 무언가를 하려면

각각의 관계를 알아야할 것 같은데

 

보통 각도라고 하면

360도 30도 90도 이렇게 알고 있을 거고

30도 각도 정도되는 꼭지를 가지고 있는 

피자 손잡이 부분은 몇 cm 정도 될까?

 

꼭지부분이 30도 일 때

손잡이 길이도 30cm 가 되면

외우기도 쉽고 좋을텐데

 

그런데 실제 피자에서 저만큼을 잘라내고 

저 손잡이 부분을 대충 줄자로 재면 30cm 가 안나오네

전체 피자판의 크기에 따라서 30cm 가 나올수도 있겠구나.

이렇게 그때 그때 다르면 규칙을 만들수가 없는데

 

그러면 실제 줄자로 측정을 해봐야겠다

어디를 측정하지? 

애매하네..

 

원의 가로지르는 길이는 평평한 자로 측정하고

원의 둘레는 줄자로 측정해보자.

 

자, 

지름이 1cm 인 원은 둘레가 3.14cm 이네.

지름이 2cm 인 원은 둘레가 6.28cm 이고

지름이 3cm 인 원은 둘레가 9.42cm 이고

지름이 4cm 인 원은 둘레가 12.72cm 이네.

이거 뭔가 규칙이 있는데?

 

지름이랑 둘레가 1 대 3.14 비율이 유지가 되네?

원이 크던 작던 지름이랑 둘레는 항상 비율이 같구나. 

지름을 알면 둘레를 알고 둘레를 측정하면 지름을 알수 있겠네?

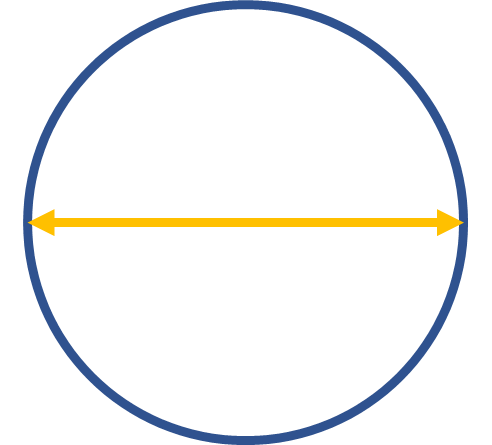
이 노란 길이보다 파란 길이는 항상 3.14 배 크다는 거구나.

이걸 매번 3.14배라고 하기 귀찮으니까 

파이라고 이름을 붙여주자.

 

노란선이 1cm일때 파란선은 파이cm

 

 

그럼 이 경우에도 파랑선이 노랑선보다 파이배 크겠네.

 

노란선이 1 일때 파란선을 파이라고 하면 되겠다.

 

 

그럼 이렇게 90도만 남겨 놓게되면

호의 길이는 파이인 3.14의 절반이니까

파이 나누기 2 인 3.14/2 가 되겠구나

대략 1.57 정도네,

 

예를 들어 반지름이 1cm 인 피자판에서

90도에 해당하는 조각을 떼어내서

손잡이를 측정하니 1.57cm 정도가 되네.

신기하다.

 

그럼 반지름이 1일때

호의 길이가 파이/2 이면 호의 각도가 파이/2 라고 정하면 편하겠네.

그런데 파이/2 면 1.57 이라며? 

너무 작은거 아냐?

1.57도?

그러면 이걸 새로운 이름으로 1.57 라디안이라고 불러야겠다.

호의 길이가 파이/2이면 호의 각도도 파이/3 라디안이 될거고 

호의 길이가 파이/4이면 호의 각도도 파이/4 라디안이 될거고

 

 

 

211212 원과 원주율 설명 그림 r1.0.pptx

0.05MB